L’objectif de cet exercice est l’étude d’une transformation cyclique à partir d’un graphique, plus précisément un diagramme de Clapeyron.
Énoncé de l’exercice
– À partir d’un graphique –
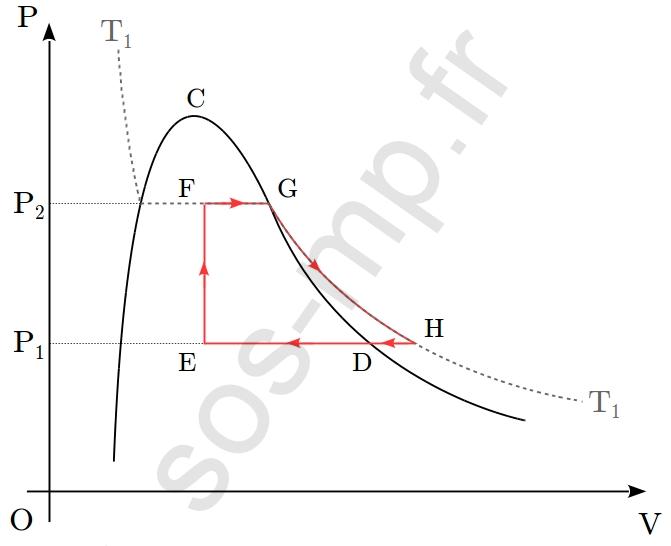
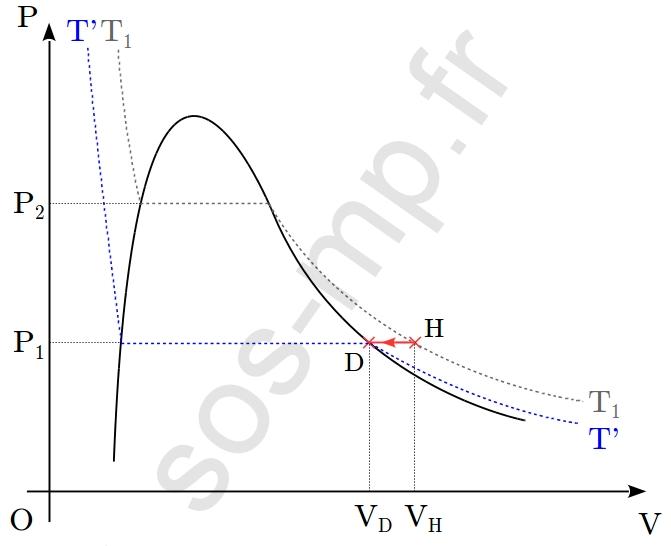
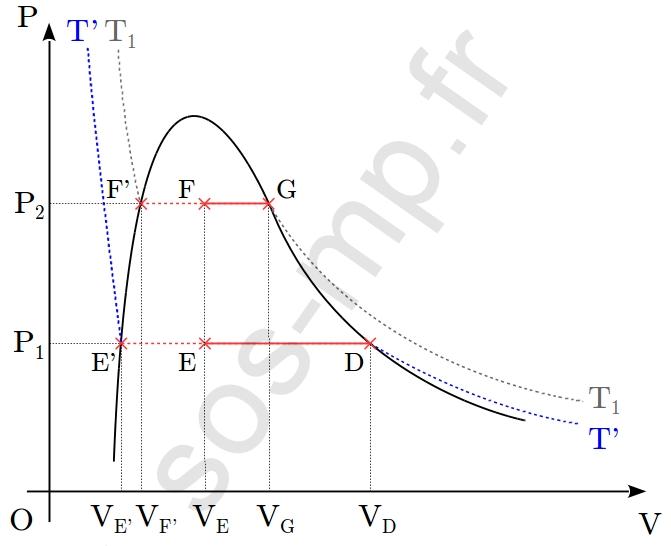
On envisage la transformation cyclique d’un système fermé, constitué d’une quantité $n$ d’un corps pur, décrite dans le diagramme de Clapeyron suivant (au sein duquel l’isotherme de température $T_1$ est représentée) :
1. Décrire chacune des transformations réalisées (D $\rightarrow$ E ; E $\rightarrow$ F ; F $\rightarrow$ G ; G $\rightarrow$ H ; H $\rightarrow$ D) en précisant notamment quels paramètres d’état restent constants ainsi que l’état physique du système.
2. Préciser la composition du système aux points E et F.
3. Estimer la valeur du volume au point H, noté, $V_\mathrm{H}$ en fonction de $V_\mathrm{G}$, sachant que $P_2=2P_1$. Justifier.
4. Estimer la valeur de la température en chacun des points, en fonction de $T_1$, sachant que $V_\mathrm{H}=1{,}2V_\mathrm{D}$.
5. Déterminer, en le justifiant, le signe des transferts thermiques algébriquement reçus par le système lors des étapes D $\rightarrow$ E, E $\rightarrow$ F et F $\rightarrow$ G.
6. Question pour la BCPST2 : déterminer le signe des transferts thermiques algébriquement reçus par le système lors des étapes G $\rightarrow$ H et H $\rightarrow$ D.
Corrigé de l’exercice
– À partir d’un graphique –

Ne pas vendre, ne pas céder, ne pas diffuser et ne pas copier cette correction sans autorisation.
Vous êtes enseignant et vous êtes intéressé par cette correction, contactez-moi.
1. Analysons chacune des transformations.
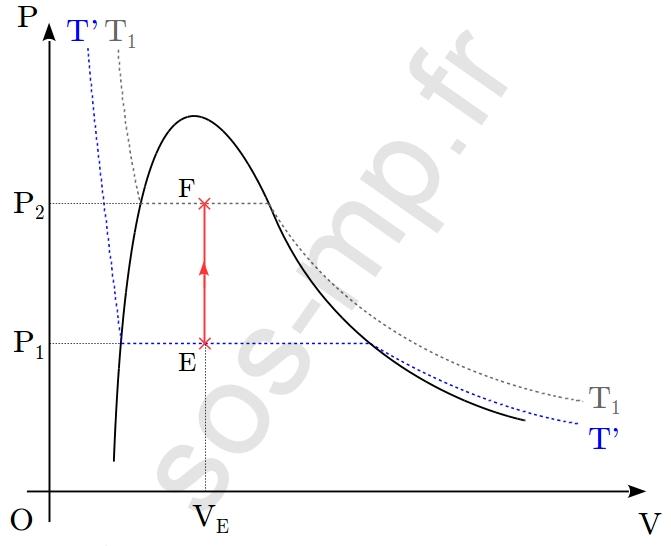
$\triangleright$ Au cours de la transformation D $\rightarrow$ E, le volume du système diminue de $V_\mathrm{D}$ à $V_\mathrm{E}$ à pression constante, égale à $P_1$. Cette transformation a lieu sur une isotherme $T’$, $(T'<T_1)$ (graphique suivant).
Ainsi les paramètres d’états restant constants lors de la transformation sont la pression, $P_1$ et la température, $T’$. Il s’agit donc d’une transformation isotherme et isobare. En D (point sur la courbe de rosée) le système est entièrement sous forme gazeuse. La diminution du volume fait alors apparaître la première goutte de liquide associé et les deux phases (liquide et gazeuse) coexistent tout au long de la transformation, jusqu’en E. Rappelons que la portion horizontale d’une isotherme est appelée palier de liquéfaction (ou de vaporisation). En parcourant totalement ce palier, à volume décroissant (croissant), le système subit une liquéfaction (vaporisation). En E, le système n’a pas subit une vaporisation complète. Il se trouve sous la forme d’un mélange liquide+gaz.
$\triangleright$ Au cours de la transformation E $\rightarrow$ F, la pression du système augmente de $P_1$ à $P_2$ à volume constant. Le point E est sur l’isotherme $T’$ et le point F sur l’isotherme $T_1>T’$ (graphique suivant).
La température à donc varié (augmenté). Ainsi le seul paramètre d’état restant constant lors de cette transformation est le volume $V$. La transformation est donc isochore.
Nous avons vu, pour le point E, que lorsque le système se trouve en un point du palier de liquéfaction (ou de vaporisation) d’une isotherme différent des points extrémités (autrement dit lorsque le point représentant le système ne se trouve pas sur la courbe de saturation), le système se trouve sous la forme d’un mélange liquide+gaz. Il en est de même au point F qui se trouve sur le palier de liquéfaction de l’isotherme $T_1$. Donc en F, le système est sous la forme d’un mélange liquide+gaz.
Remarque : nous verrons à la question 2. que cette transformation consiste en une vaporisation (une fraction de la phase liquide du système passe à l’état gazeux).
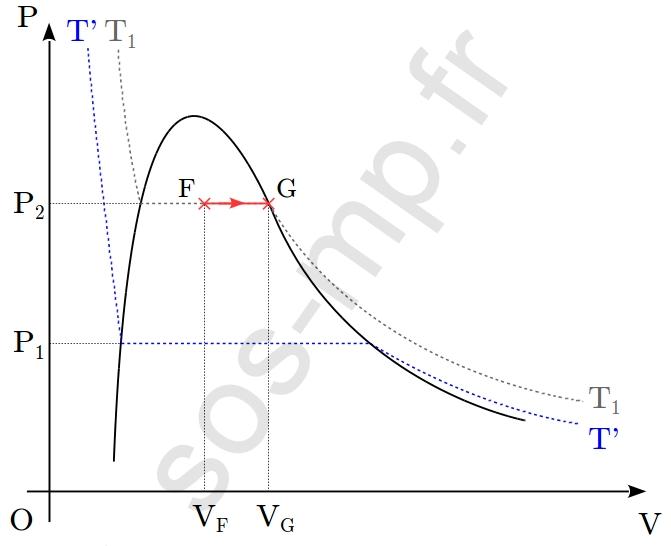
$\triangleright$ Au cours de la transformation F $\rightarrow$ G, le volume du système augmente de $V_\mathrm{F}$ à $V_\mathrm{G}$ à pression constante, égale à $P_2$. Cette transformation a lieu sur l’isotherme $T_1$ (graphique suivant).
Ainsi les paramètres d’états restant constants lors de la transformation sont la pression, $P_2$ et la température, $T_1$. Il s’agit donc d’une transformation isotherme et isobare. En F (point sur le palier de liquéfaction ou de vaporisation) le système est sous la forme d’un mélange liquide+gaz. En G (point sur la courbe de rosée) le système est entièrement sous forme gazeuse. Au cours de cette transformation, de F à G, le système subit une vaporisation (complète).
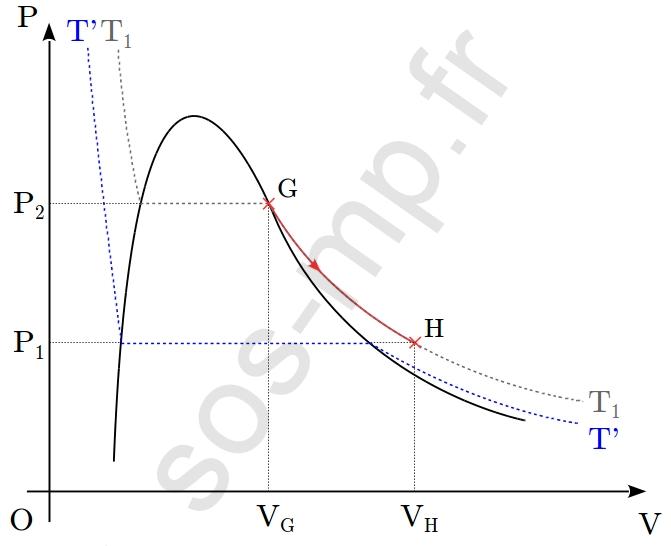
$\triangleright$ Au cours de la transformation G $\rightarrow$ H, le volume du système augmente de $V_\mathrm{G}$ à $V_\mathrm{H}$ et le volume diminue de $P_2$ à $P_1$. Cette transformation a lieu le long de l’isotherme $T_1$ (graphique suivant).
Ainsi, le seul paramètre d’état à rester constant lors de cette transformation est la température, égale à $T_1$. Il s’agit donc d’une transformation isotherme. En G, ainsi qu’en H, le système est sous forme gazeuse. La transformation subit par le gaz est une détente (augmentation du volume et diminution de la pression) isotherme.
$\triangleright$ Au cours de la transformation H $\rightarrow$ D, le volume du système diminue de $V_\mathrm{H}$ à $V_\mathrm{D}$ à pression constante, égale à $P_1$. Le point H est sur l’isotherme $T_1$ et le point D sur l’isotherme $T'<T_1$ (graphique suivant).
Ainsi, le seul paramètre à rester constant est la pression, égale à $P_1$. La transformation est donc isobare. En H, ainsi qu’en D, le système est sous forme gazeuse. La transformation subit par le gaz est une compression isobare.
2. Préciser la composition du système aux points E et F, où le système est sous la forme d’un mélange liquide+gaz, signifie donner la proportion des phases dans le mélange. Comme nous ne disposons d’aucune donnée numérique, il nous reste à exploiter le graphique (graphique suivant) et convoquer le théorème des moments.
D’après le théorème des moments, les fractions molaires liquide et gazeuse, en E, sont respectivement
$\displaystyle x_\mathrm{liq}(\mathrm{E})=\frac{n_\mathrm{liq}}{n_\mathrm{tot}}=\frac{V_\mathrm{D}-V_\mathrm{E}}{V_\mathrm{D}-V_\mathrm{E’}}=\frac{\mathrm{ED}}{\mathrm{E’D}}\quad $ et $\quad \displaystyle x_\mathrm{gaz}(\mathrm{E})=1-x_\mathrm{liq}(\mathrm{E})=\frac{\mathrm{E’E}}{\mathrm{E’D}}$
En mesurant $\mathrm{ED}$ et $\mathrm{E’E}$, longueurs respectives des segments $[\mathrm{ED}]$ et $[\mathrm{E’E}]$ sur le graphique, à savoir $\mathrm{ED}=30~\mathrm{mm}$ et $\mathrm{E’E}=45~\mathrm{mm}$, nous obtenons la fraction molaire liquide, en $\mathrm{E}$ :
$\displaystyle x_\mathrm{liq}(\mathrm{E})=\frac{\mathrm{ED}}{\mathrm{E’D}}=\frac{30}{45}=\frac{2}{3}\simeq 0{,}67$
D’où, $\boxed{x_\mathrm{liq}(\mathrm{E})=67~\%}$.
Nous en déduisons la fraction molaire de la phase gazeuse en $\mathrm{E}$ :
$\boxed{x_\mathrm{gaz}(\mathrm{E})=1-x_\mathrm{liq}(\mathrm{E})=33~\%}$
En faisant de même au point $\mathrm{F}$, nous obtenons $\mathrm{FG}=12{,}5~\mathrm{mm}$ et $\mathrm{F’G}=25~\mathrm{mm}$, d’où les fractions molaires des phases en $\mathrm{F}$ :
$\boxed{x_\mathrm{liq}(\mathrm{F})= 50~\%} \quad$ et $\quad \boxed{x_\mathrm{gaz}(\mathrm{F})= 50~\%}$
Nous pouvons constater qu’au passage de l’état $\mathrm{E}$ à l’état $\mathrm{F}$, la fraction molaire de la phase gazeuse à augmentée, passant de $33~\%$ à $50~\%$. La transformation $\mathrm{E} \rightarrow \mathrm{F}$ est une donc vaportisation.
3. La tranformation $\mathrm{G} \rightarrow \mathrm{H}$ décrite plus haut (question 1.) se produit à température constante, égale à $T_1$. Le système est sous forme gazeuse tout au long de la transformation. En considérant la phase gazeuse comme un gaz parfait, nous avons, d’après la loi de Boyle-Mariotte appliquée entre $\mathrm{G}$ et $\mathrm{H}$ :
$$P_\mathrm{G}V_\mathrm{G}=P_\mathrm{H}V_\mathrm{H}$$
Soit
$$V_\mathrm{H}=\frac{P_\mathrm{G}V_\mathrm{G}}{P_\mathrm{H}}=\frac{P_2V_\mathrm{G}}{P_1}=\frac{2P_1V_\mathrm{G}}{P_1}=2V_\mathrm{G}$$
Ainsi, $\boxed{V_\mathrm{H}=2V_\mathrm{G}}$.
4. Déterminons la température aux points $\mathrm{D}$, $\mathrm{E}$, $\mathrm{F}$, $\mathrm{G}$ et $\mathrm{H}$.
Puisque les point $\mathrm{F}$, $\mathrm{G}$ et $\mathrm{H}$ sont tous les trois sur l’isotherme $T_1$, nous avons déjà
$$\boxed{T_\mathrm{F}=T_\mathrm{G}=T_\mathrm{H}=T_1}$$
De même, les point $\mathrm{D}$ et $\mathrm{E}$ se trouve sur une même isotherme, donc $T_\mathrm{D}=T_\mathrm{E}$. Il nous faut relier cette température à $T_1$.
On nous donne $V_\mathrm{H}=1{,}2V_\mathrm{D}$. Nous avons de plus, $P_\mathrm{D}=P_\mathrm{H}=P_1$ et $T_\mathrm{H}=T_1$. Il nous semble pouvoir relier $T_\mathrm{D}$ à $T_\mathrm{H}$ autrement dit à $T_1$.
Pour ce faire, exprimons à nouveau la loi des gaz parfaits en $\mathrm{H}$ et en $\mathrm{D}$. Nous obtenons
en $\mathrm{H}$ : $\quad P_1V_\mathrm{H}=nRT_1 \quad (1)$
en $\mathrm{D}$ : $\quad P_1V_\mathrm{D}=nRT_\mathrm{D} \quad (2)$
Puis, faisons le rapport $\displaystyle \frac{(2)}{(1)}$. Après simplification, nous obtenons
$$\begin{eqnarray} \frac{V_\mathrm{D}}{V_\mathrm{H}}=\frac{T_\mathrm{D}}{T_1} \quad &\Longleftrightarrow& \quad \frac{V_\mathrm{D}}{1{,}2V_\mathrm{D}}=\frac{T_\mathrm{D}}{T_1} \nonumber \\ &\Longleftrightarrow& \quad T_\mathrm{D}=\frac{T_1}{1{,}2} \nonumber\end{eqnarray} $$
D’où,
$$\boxed{T_\mathrm{D}=T_\mathrm{E}=\frac{T_1}{1{,}2}}$$
Remarque : ce résultat confirme ce que nous avions obtenu pour la description de la transformation $\mathrm{H} \rightarrow \mathrm{D}$, à savoir que $T_\mathrm{D}=T'<T_1$.
5. Nous avons vu que la transformation $\mathrm{D} \rightarrow \mathrm{E}$ est une liquéfaction isotherme et isobare. Or la liquéfaction est un changement d’état exothermique, c’est-à-dire qui libère de la chaleur. L’énergie thermique est donc fournie par le système au milieu extérieur. D’où un transfert thermique algébriquement reçu par le système lors de la transformation $\mathrm{D} \rightarrow \mathrm{E}$
$$\boxed{Q_{\mathrm{D}\rightarrow \mathrm{E}}<0}$$
Nous avons vu que la transformation $\mathrm{E} \rightarrow \mathrm{F}$ consiste en la vaporisation d’une partie du liquide avec augmentation de la température. Une vaporisation étant une transformation endothermique, l’énergie est fournie par le milieu extérieur et reçu par le système. On a ainsi
$$\boxed{Q_{\mathrm{E}\rightarrow \mathrm{F}}>0}$$
Enfin, la transformation $\mathrm{F} \rightarrow \mathrm{G}$ est une vaporisation isotherme et isobare. De même,
$$\boxed{Q_{\mathrm{F}\rightarrow \mathrm{G}}>0}$$
6. La transformation $\mathrm{G} \rightarrow \mathrm{H}$ est une détente (augmentation du volume avec diminution de la pression) isotherme.
Or, pour un gaz parfait (nous faisons l’hypothèse du gaz parfait), la variation d’énergie interne est $\Delta U=mC_\mathrm{v} \Delta T$. Autrement dit, pour une gaz parfait, la variation d’énergie interne lors d’une transformation ne dépend que de la variation de température. Ceci implique donc qu’une transformation isotherme $(\Delta T=0)$ laisse inchangée l’énergie interne du gaz $(\Delta U=0)$.
Ainsi, pour la transformation isotherme $\mathrm{G} \rightarrow \mathrm{H}$, on a , d’après le premier principe de la thermodynamique :
$$\Delta U_{\mathrm{G} \rightarrow \mathrm{H}}=W_{\mathrm{G} \rightarrow \mathrm{H}}+Q_{\mathrm{G} \rightarrow \mathrm{H}}=0$$
soit $Q_{\mathrm{G} \rightarrow \mathrm{H}}=-W_{\mathrm{G} \rightarrow \mathrm{H}}$.
Or, s’agissant d’un détente, le système fournit du travail au milieu extérieur, d’où $W_{\mathrm{G} \rightarrow \mathrm{H}}<0$.
On a donc finalement
$$\boxed{Q_{\mathrm{G}\rightarrow \mathrm{H}}>0}$$
La transformation $\mathrm{H} \rightarrow \mathrm{D}$, elle, est isobare. Aucun transfert de travail mécanique n’a lieu entre le système et le milieu extérieur. Donc $W_{\mathrm{H}\rightarrow \mathrm{D}}=0$
Ainsi, toujours d’après le premier principe de la thermodynamique,
$$\Delta U_{\mathrm{H} \rightarrow \mathrm{D}}=W_{\mathrm{H} \rightarrow \mathrm{D}}+Q_{\mathrm{H} \rightarrow \mathrm{D}}=Q_{\mathrm{H} \rightarrow \mathrm{D}}$$
De plus, comme nous l’avons vu, la température diminue au cours de la transformation. Cela implique que $\Delta T_{\mathrm{H} \rightarrow \mathrm{D}}<0$ et donc que $\Delta U_{\mathrm{H} \rightarrow \mathrm{D}}<0$. Donc
$$\boxed{Q_{\mathrm{H} \rightarrow \mathrm{D}}<0}$$
Si besoin, consultez les cours de BCPST1 de M Nicolas Clatin sur :
- Description d’un système thermodynamique
- Transfert d’énergie ; travail et chaleur
- Changement d’état du corps pur