Cet exercice a pour but la détermination expérimentale des paramètres d’un circuit RL série soumis à un échelon de tension. Pour cela vous avez à votre disposition les relevés
- de l’intensité du courant circulant dans le circuit en fonction du temps ;
- de la dérivée par rapport au temps de la tension aux bornes du résistor en fonction de cette dernière.
Énoncé de l’exercice
– Détermination expérimentale des paramètres d’un circuit RL –
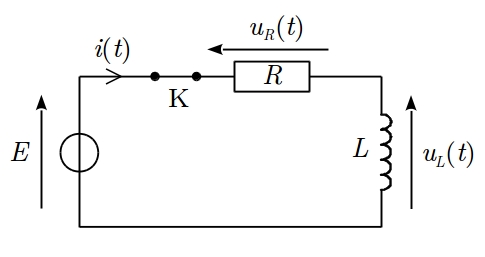
Un dipôle $\mathrm{RL}$ est relié à $t=0$ à un générateur idéal de tension à vide $E$. On obtient les relevés expérimentaux ci-dessous.
1. Commentez les graphiques obtenus.
2. Déterminez graphiquement les valeurs de $R$, $L$ et $E$ et de la constante de temps $\tau$.
Corrigé de l’exercice
– Détermination expérimentale des paramètres d’un circuit RL –

Vous êtes enseignant et vous êtes intéressé par cette correction, contactez-moi.
$\triangleright$ Pour $t<0$, l’interrupteur $\mathrm{K}$ est ouvert. Nous avons donc le circuit suivant
Le circuit série étant ouvert, aucun courant n’y circule. Donc $i(t<0)=0$. Nous avons alors
$u_\mathrm{R}(t<0)=Ri(t<0)=0$ et $\displaystyle u_\mathrm{L}=L\frac{\mathrm{d}i(t<0)}{\mathrm{d}t}=0$
$\triangleright$ À $t=0$, on ferme l’interrupteur. Le dipôle RL est alors soumis à la tension $E$.
$\triangleright$ Pour $t>0$, on a donc le circuit
1. Commentaire du graphique de $i(t)$.
$i(t)$ représente l’intensité du courant dans le circuit, à savoir, puisqu’il s’agit d’un circuit en série, le courant traversant à la fois le résistor $R$ et la bobine $L$.
$\bullet$ Nous savons que l’intensité du courant qui traverse une bobine est continue dans le temps. $i(t)$ est donc continue et en particulier en $t=0$. On a donc nécessairement $i(t=0^-)=i(t=0^+)=i(t=0)$.
Or, $i(t<0)=0$ qui implique que $i(t=0^-)=0$. Donc, $i(t=0^+)=i(t=0^-)=i(t=0)=0$.
C’est bien ce que l’on observe sur le graphique : la courbe représentant $i(t)$ passe par l’origine du repère.
$\bullet$ Ensuite quand $t\rightarrow \infty$, le régime transitoire est terminé et l’on se trouve en régime stationnaire. L’intensité du courant dans la bobine est donc constant et la tension à ses bornes, $\displaystyle u_\mathrm{L}=L\frac{\mathrm{d}i}{\mathrm{d}t}=0$.
La loi des mailles appliquée au circuit donne
$E-u_\mathrm{R}-u_\mathrm{L}=0$.
Soit, puisque $u_\mathrm{L}=0$
$\displaystyle E=u_\mathrm{R}=Ri \quad \Longleftrightarrow \quad i=\frac{E}{R}=\mathrm{cste}$.
Ainsi, $\displaystyle \lim_{t \rightarrow \infty}i(t)=\frac{E}{R}=\mathrm{cste}$.
C’est bien ce que l’on observe sur le graphique. La courbe de $i(t)$ admet bien une asymptote horizontale d’équation $\displaystyle y=\frac{E}{R}$.
$\bullet$ Pour finir, déterminons l’expression de $i(t)$ pour tout $t$.
Appliquons la loi des mailles à un instant $t$ fini quelconque. Nous obtenons
$\begin{eqnarray} && \quad E-u_\mathrm{R}-u_\mathrm{L}=0 \nonumber \\ &\Longleftrightarrow& \quad E=u_\mathrm{R}+u_\mathrm{L} \nonumber \\ &\Longleftrightarrow& \quad E=Ri+L\frac{\mathrm{d}i}{\mathrm{d}t} \nonumber \\ &\Longleftrightarrow& \quad \frac{\mathrm{d}i}{\mathrm{d}t}+\frac{R}{L}i=\frac{E}{L} \nonumber \\ &\Longleftrightarrow& \quad \frac{\mathrm{d}i}{\mathrm{d}t}+\frac{i}{\tau}=\frac{E}{L} \nonumber \qquad (1) \end{eqnarray}$
avec $\displaystyle \tau=\frac{L}{R}$.
L’équation différentielle $(1)$ modélise l’évolution de $i$ en fonction du temps. Pour déterminer $i(t)$ pour tout $t$, résolvons cette équation.
Il s’agit d’une équation différentielle linéaire du premier ordre avec second membre et à coefficients constants. La solution générale de cette équation est la somme de la solution de son équation homogène associée et d’une solution particulière. On obtient (voir cours) :
$$i(t)=A\mbox{e}^{\displaystyle -\frac{t}{\tau}}+\frac{E}{R}$$
avec $A$ une constante d’intégration à déterminer.
Pour cela, on a $\displaystyle i(t=0)=A+\frac{E}{R}$, soit $\displaystyle A=-\frac{E}{R}$.
Soit finalement
$$i(t)=\frac{E}{R}\left(1-\mbox{e}^{\displaystyle -\frac{t}{\tau}}\right)$$
Pour étudier les variation de la fonction $i(t)$, dérivons-la. Nous obtenons
$$\frac{\mathrm{d}i}{\mathrm{d}t}=\frac{E}{R\tau}\mbox{e}^{\displaystyle -\frac{t}{\tau}}>0$$
$i(t)$ est donc croissante (sa dérivée étant positive).
C’est bien ce que l’on observe sur le graphique.
De plus,
$$\frac{\mathrm{d}^2i}{\mathrm{d}t^2}=-\frac{E}{R\tau^2}\mbox{e}^{\displaystyle -\frac{t}{\tau}}<0$$
$i(t)$ est donc strictement concave. C’est bien ce que l’on observe sur le graphique.
Commentaire du graphique de $\displaystyle \frac{\mathrm{d}u_\mathrm{R}}{\mathrm{d}t}(u_\mathrm{R})$.
À tout instant $t$ la loi d’Ohm donne $u_\mathrm{R}=Ri$. Soit $\displaystyle i=\frac{u_\mathrm{R}}{R} \qquad (2)$.
En substituant $(2)$ dans $(1)$, on obtient
$\begin{eqnarray}&& \quad \frac{\mathrm{d}\left(\displaystyle\frac{u_\mathrm{R}}{R}\right)}{\mathrm{d}t}+\frac{\displaystyle \frac{ u_\mathrm{R}}{R}}{\tau}=\frac{E}{L} \nonumber \\ &\Longleftrightarrow& \quad \frac{1}{R}\frac{\mathrm{d}u_\mathrm{R}}{\mathrm{d}t}+\frac{1}{\tau}\frac{u_\mathrm{R}}{R}=\frac{E}{L} \nonumber \\ &\Longleftrightarrow& \quad \frac{\mathrm{d}u_\mathrm{R}}{\mathrm{d}t}+\frac{u_\mathrm{R}}{\tau}=\frac{RE}{L} \nonumber \\ &\Longleftrightarrow& \quad \frac{\mathrm{d}u_\mathrm{R}}{\mathrm{d}t}=-\frac{u_\mathrm{R}}{\tau}+\frac{RE}{L} \nonumber\end{eqnarray}$
Ainsi, $\displaystyle \frac{\mathrm{d}u_\mathrm{R}}{\mathrm{d}t}$ est une fonction affine de $u_\mathrm{R}$ de coefficient directeur $\displaystyle -\frac{1}{\tau}<0=-\frac{R}{L}$ et d’ordonnée à l’origine $\displaystyle \frac{ER}{L}>0$.
On observe bien comme courbe représentative, sur le graphique, une droite de pente négative et d’ordonnée à l’origine positive.
2. Détermination graphique des valeurs de $R$, $L$, $E$ et $\tau$.
Pour cela, il faut exploiter les graphiques et les valeurs numériques qui s’y trouvent. Les valeurs apparaissant dans les graphiques ne correspondent pas directement aux valeurs des grandeurs recherchées. Mais elles en dépendent. Il faut donc exprimer ces relations de dépendance. Autrement dit, obtenir les équations qui, par résolution conduiront aux valeurs recherchées. Intéressons-nous aux valeurs de $R$, $L$ et $E$. La valeur de $\tau=\frac{L}{R}$ en sera ensuite déduite. Nous avons trois inconnues, il nous faut donc trois équations indépendantes.
$\triangleright$ Commençons par exploiter le graphique de $i(t)$.
Il a été montré en 1., que $\displaystyle \displaystyle \lim_{t \rightarrow \infty}i(t)=\frac{E}{R}$ ce qui nous donne
$$\frac{E}{R}=10~\mbox{mA}=10\times 10^{-3}~\mbox{A}$$
$\triangleright$ Maintenant, exploitons le graphique de $\displaystyle \frac{\mathrm{d}u_\mathrm{R}}{\mathrm{d}t}(u_\mathrm{R})$.
De même, nous avons obtenu plus haut (en 1.) que
- l’ordonnée à l’origine de la droite représentant $\displaystyle \frac{\mathrm{d}u_\mathrm{R}}{\mathrm{d}t}$ en fonction de $u_\mathrm{R}$ est $\displaystyle \frac{ER}{L}$ ;
- et que son coefficient directeur est $\displaystyle -\frac{1}{\tau}=-\frac{R}{L}$.
L’ordonnée à l’origine s’obtient graphiquement :
$$\frac{ER}{L}=25~\mbox{V}\cdot \mbox{ms}^{-1}= 25\times 10^3~\mbox{V}\cdot \mbox{s}^{-1}$$
et le coefficient directeur
$$-\frac{R}{L}=\frac{\Delta y}{\Delta x}=\frac{0-25}{5-0}=-5~\mbox{ms}^{-1}=-5\times 10^3~\mbox{s}^{-1}$$
D’où
$$\frac{R}{L}=5\times 10^3~\mbox{s}^{-1}$$
Il nous reste à résoudre le système suivant :
$$\left\{\begin{eqnarray} && \frac{E}{R}=10\times 10^{-3}~\mbox{A} \qquad (3) \nonumber \\ &&\frac{ER}{L}= 25\times 10^3~\mbox{V}\cdot \mbox{s}^{-1} \qquad (4) \nonumber \\ &&\frac{R}{L}=5\times 10^3~\mbox{s}^{-1} \qquad (5) \nonumber \end{eqnarray}\right.$$
$(5)$ dans $(4)$ donne
$$E=\frac{25\times 10^3}{\frac{R}{L}}=\frac{25\times 10^3}{5\times 10^3} \qquad \Longleftrightarrow \qquad \boxed{E=5~\mbox{V}}$$
ce qui conduit avec $(3)$ à
$$R=\displaystyle \frac{E}{10\times 10^{-3}}=\frac{5}{10\times 10^{-3}} \qquad \Longleftrightarrow \qquad \boxed{R=500~\Omega} $$
puis avec $(5)$ à
$$L=\frac{R}{5\times 10^3}=\frac{500}{5\times 10^3} \qquad \Longleftrightarrow \qquad \boxed{L=0{,}1~\mbox{H}}$$
Constante de temps $\tau$
Puisque $\displaystyle \tau=\frac{L}{R}$, nous en déduisons que
$$\tau=\frac{L}{R}=\frac{0{,}1}{500}=2\times 10^{-4}~\mbox{s}\qquad \Longleftrightarrow \qquad \boxed{\tau=0{,}2~\mbox{ms}}$$
$\tau$ aurait pu aussi être déterminer graphiquement. Puisque nous savons que la tangente à l’origine de la courbe $i(t)$ coupe l’asymptote horizontale au point d’abscisse $t=\tau$ :