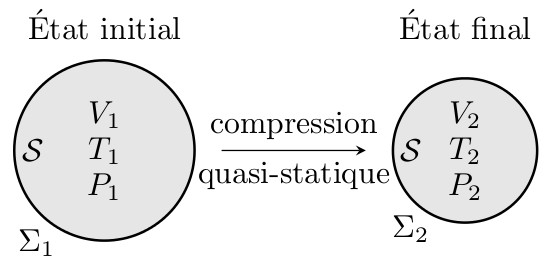
Cet exercice est assez classique. Il s’agit d’appliquer le premier principe de la thermodynamique sur un système constitué d’un certain volume de gaz parfait afin de déterminer le travail fourni lors d’une transformation quasi-statique et d’en déduire la puissance d’une pompe.
Énoncé de l’exercice
– Puissance d’une pompe –
Calculer la puissance d’une pompe servant à comprimer quasi-statiquement à la température constante de $0^\circ\mathrm{C}$ $1{,}00~\mathrm{m}^3$ d’air par minute de $1{,}0~\mathrm{atm}$ à $3{,}5~\mathrm{atm}$ $(1~\mathrm{atm}=1{,}013\cdot 10^{5}~\mathrm{Pa}).$
Corrigé de l’exercice
– Puissance d’une pompe –

Si besoin, consultez les cours de BCPST1 de M Nicolas Clatin sur :
- Description d’un système thermodynamique
- Transfert d’énergie : travail et chaleur
- Premier principe de la thermodynamique : énergie interne et enthalpie